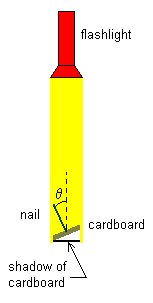
Shine a flashlight onto a card. Notice how the size of the shadow on your desk depends on the oreientation of the card with respect to the beam of light. Come up with a formula that describes how much light was being blocked by the card.
Each group needs: flashlight, small piece of cardboard, nail (2-3" with large head), protractor, ruler, meterstick
- How do you define the
orientation of a plane surface? Discuss with your group.
- Make a drawing that shows
how you could use a nail and a piece of cardboard to represent a unit of area.
What angle should be used to define the orientation of the surface?
- State which orientation
of the nail and the beam of light represents 0°. Which represents 180°?
- Hold the flashlight approximately
one meter above the table and shine light from the flashlight down onto the
cardboard held near the table.
- Vary the angle of the
cardboard and measure the area of the shadow on the table. Do this for ten
angles between 0° and 180°. (Is there an easy way to measure the angle?) Which
variables must you hold constant while taking these measurements?
- Sketch a graph of the
area of the shadow versus angle. The shadow indicates the amount of light
flux, or the light intercepted by the cardboard. What mathematical model represents your
results?
University
of Pittsburgh