


Next: Activity on Non-Equilibrium Quantum
Up: cv
Previous: Experience
In the last years I have mostly worked on
Out-of-Equilibrium Quantum Field Theory and its applications.
Out-of-Equilibrium QFT is especially needed in the study of the Early
Universe Physics and in Heavy Ion collisions since in these
situations the time evolution of the system is so rapid
that a local thermodynamical equilibrium assumption cannot hold;
moreover a full relativistic treatment is needed.
For sake of discussion, Out of Equilibrium QFT can
be split into two different
realms: the realm of systems strongly out of equilibrium and the realm
of systems weakly of equilibrium. Both from the physical and the
technical point of view, the two realms are very different and are
studied with completely different tools. As it can be expected,
strongly out of equilibrium systems are much more difficult to study
and their analysis is at the very beginning. The systems where
we have the most of information and understanding are simple
systems containing scalar fields, like the 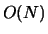 linear
sigma-model which has been understood well enough in the large
linear
sigma-model which has been understood well enough in the large 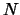 limit, or in similar frameworks such as the Hartree-Fock
approximation, where the theory is gaussian-like [1], at
least for homogeneous systems. The non-homogeneous situation is numerically
challenging but within the reach of present day computers [3].
The study of
next-to-leading corrections has been started very recently and it looks very
promising [2]; the same can be
said for what concerns even the leading order in
limit, or in similar frameworks such as the Hartree-Fock
approximation, where the theory is gaussian-like [1], at
least for homogeneous systems. The non-homogeneous situation is numerically
challenging but within the reach of present day computers [3].
The study of
next-to-leading corrections has been started very recently and it looks very
promising [2]; the same can be
said for what concerns even the leading order in 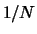 for more
complicate systems like Yukawa systems or quantum electrodynamics.
On the other hand, much more has been understood in the case of
weakly out of equilibrium systems, in which there are standardized
methods to attack the problem. The fundamental tool to perform the
study of weakly out of equilibrium systems is linear
response theory. Consider a system near equilibrium, i.e. with a
density matrix equal to a thermal density matrix except for a
small disturbance, which can be imputed to the presence of a set
of small external sources
for more
complicate systems like Yukawa systems or quantum electrodynamics.
On the other hand, much more has been understood in the case of
weakly out of equilibrium systems, in which there are standardized
methods to attack the problem. The fundamental tool to perform the
study of weakly out of equilibrium systems is linear
response theory. Consider a system near equilibrium, i.e. with a
density matrix equal to a thermal density matrix except for a
small disturbance, which can be imputed to the presence of a set
of small external sources 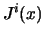 coupled to the fundamental
fields
coupled to the fundamental
fields 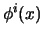 of the system. The only non-equilibrium effects,
neglecting quadratic effects in
of the system. The only non-equilibrium effects,
neglecting quadratic effects in  , are in the evolution of one-point
functions
, are in the evolution of one-point
functions
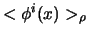 and two-point functions
and two-point functions
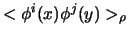 . Since the density matrix is nearly
thermal, methods of thermal field theory
can be used and the evolution can be studied in principle by using
perturbation theory, i.e. by computing thermal Feynman diagrams. The
difficulties come from severe infrared divergences which invalidate naive
perturbation theory and require resummation of infinite sets of
diagrams. Eventually, under certain conditions, the effect of this
resummation is believed to be equivalent to a phenomenological
effective classical kinetic theory, based on a quantum-relativistic
Boltzmann equation. However the precise correspondence within the
classical theory and the underlying quantum field theory is not
very well understood, except in the case of the
. Since the density matrix is nearly
thermal, methods of thermal field theory
can be used and the evolution can be studied in principle by using
perturbation theory, i.e. by computing thermal Feynman diagrams. The
difficulties come from severe infrared divergences which invalidate naive
perturbation theory and require resummation of infinite sets of
diagrams. Eventually, under certain conditions, the effect of this
resummation is believed to be equivalent to a phenomenological
effective classical kinetic theory, based on a quantum-relativistic
Boltzmann equation. However the precise correspondence within the
classical theory and the underlying quantum field theory is not
very well understood, except in the case of the 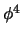 theory
[4]. In my work, I was particularly interested in studying
situations under which the kinetic approximation fails, the
approach to thermalization is subtle and non-equilibrium effects
are expected to play a major role.
theory
[4]. In my work, I was particularly interested in studying
situations under which the kinetic approximation fails, the
approach to thermalization is subtle and non-equilibrium effects
are expected to play a major role.
Subsections



Next: Activity on Non-Equilibrium Quantum
Up: cv
Previous: Experience
Michele Simionato
2003-03-07