Activity on Wilson Renormalization Group

My scientific activity during my Ph. D. years was about gauge theories in the Wilson Renormalization Group Approach. In particular I refer here to a recent formulation in which one studies the Exact Renormalization Group Equation (ERGE) of the Euclidean one-particle-irreducible effective action 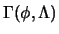$\Gamma(\phi,\Lambda)$ where the Wilsonian scale 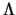$\Lambda$ is interpreted as an infrared cutoff. This is a more elegant formulation of the Wilson's renormalization group equation (others well known forms of the evolution equation where given by Wegner and Houghton and by Polchinski) first introduced (independently) by Wetterich [7] and Bonini, D'Attanasio, Marchesini [8]. 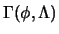The equation for the Wilsonian effective action can be obtained from the equation for the 1PI effective action via a Legendre transformation and they are mathematically equivalent; however for many applications, both perturbative and non-perturbative, the equation on $\Gamma(\phi,\Lambda)$ is much more convenient. While the nonperturbative analysis of the ERGE equation (with particular interest to the computation of critical exponents in three-dimensional scalar theories) have been extensively studied by many authors [9], the perturbative expansion has been the preferred subject of study of Bonini and Marchesini and collaborators, including myself, as well of others [10]. A great advantage of the perturbative studies, is that it is possible to have a clear understanding of the problems encountered in extending the Wilsonian formalism to gauge theories, i.e. the problems due to the breaking of gauge-invariance. In particular, in perturbation theory it is possible to solve the so-called fine-tuning equations which say how to fix the ultraviolet non-invariant action in terms of renormalized parameters in such a way than the physical action becomes consistent with the gauge-symmetry (i.e. with the Ward-Takahashi or Slavnov-Taylor identities). My Ph. D. thesis consisted in the analysis of the consistency of suitable approximation schemes for solving the evolution equation for gauge theories in the perturbative region, by implementing some kind of resummation, i.e. expanding in terms of a scale-dependent coupling constant.

• [REN] Beta function and flowing coupling in the exact Wilson renormalization group in Yang-Mills theory, M. Bonini, G. Marchesini and M. Simionato, UPRF-96-464, IFUM-525-FT, hep-th/9604114, 19pp. Published in Nucl. Phys. B483 (1997) 475. In this paper we introduced a general scheme to generate an improved (resummed) perturbative solution of the ERGE and we applied it to QCD. We shown that in this context the infrared Landau pole can be avoided, giving support to the view that it is only an artifact of the usual RG-improved perturbation theory. The philosophy is that it should be possible to define a kind of effective running constant well behaved in the infrared. This is indeed the case in the Wilsonian approach. However the problem of the approach as presented here was the consistency with gauge-invariance. To elucidate this problem we studied in detail the case of abelian gauge theories in the (unpublished) paper [BS] Wilson renormalization group and improved perturbation theory, M. Bonini, M. Simionato, UPRF-97-05, hep-th/9705146, 24pp. There we shown that the improved perturbation theory is indeed consistent with gauge-invariance, at the physical scale 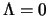$\Lambda=0$ even if in the loop computations one uses a Ward identities-breaking infrared cutoff.
• [QED]Gauge Consistent Wilson Renormalization Group I: The Abelian Case, M. Simionato, UPRF-98-08, LPTHE-98-08, hep-th/9809004, 34pp. Published in Int.J. Mod. Phys. A15:2121, 2000. Motivated by the need to improve the formulation in [REN], which cannot be easily implemented in the non-abelian case beyond the one-loop level, in this paper I have reconsidered the abelian-case. The essential point was to recognize that the simplest way to introduce an infrared cutoff in a theory, i.e. by giving a mass to all massless fields, can be reinterpreted in a Wilsonian way (this is non-trivial, however, since the would-be ERGE requires an explicit ultraviolet regularization in order to be well defined). Then the ERGE can be immediately identified with the Callan-Symanzik equation. The big advantage of this formulation is that it is consistent with the Ward-Takahashi identities to all orders in perturbation theory.
• [NC]Gauge Consistent Wilson Renormalization Group II: The Non-Abelian Case, M. Simionato, UPRF-98-10, LPTHE-98-10, hep-th/
  9810117, 33pp. Published in Int.J. Mod. Phys. A15:2153, 2000. The other advantage of the formulation introduced in [QED] relies on the fact that it can be extended to the non-abelian case provided we work in algebraic noncovariant gauges. The crucial point is that the introduction of the Wilsonian infrared cutoff as a mass term for the gauge field minimize the problem of the gauge-symmetry breaking, which is harmless in the gauge of non-covariant gauge-fixing, in the sense that the Ward-Takahashi identities are preserved to all scales. Moreover renormalizability and unitarity are preserved, but not the Lorentz-covariance, which is broken, at 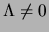$\Lambda\neq0$, even for would be physical quantities. This is the reason why the infrared cutoff must be removed, at the very end, in order to recover the physical theory.
• [ANC]On the Consistency of the Exact Renormalization Group Approach Applied to Gauge Theories in Algebraic Non-Covariant Gauges, M. Simionato, LPTHE-00-18, hep-th/0005083, 48pp. Published in Int. J. Mod. Phys. A15:4811, 2000. Since algebraic noncovariant gauges are typically very subtle and very singular, at least in perturbative applications, I performed a careful study of the infrared limit 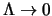$\Lambda\to0$ in various gauges. In particular, I found that the perturbative expansion in the axial gauge is plagued by unphysical infrared divergences in the 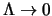$\Lambda\to0$ limit, which appears even in the computation of a would be physical quantity like the Wilson loop corresponding to the interquark potential. On the contrary, as expected, the light-cone gauge with the Mandelstan-Leibbrandt prescriprions, which comes automatically in the Wilsonian formalism, is perfectly consistent and well behaved with respect to the perturbative expansion. The the program of [REN] can be successfully implemented.