


Next: Activity on Wilson Renormalization
Up: Scientific Activity
Previous: Activity on Non-Equilibrium Quantum
I give now a short descriptions of my papers on (near) Equilibrium
QFT, made in collaborations involving H.J. De Vega (LPTHE, Paris),
D. Boyanovsky (University of Pittsburgh), R. Holman
(Carnegie Mellon University).
- [DRG]Dynamical Renormalization Group Resummation of
Finite Temperature Infrared Divergences,
D. Boyanovsky, H. J. De Vega, R. Holman, M. Simionato, LPTHE-98-08,
PITT-98-08, hep-ph/9809346, 36pp. Published in Phys. Rev. D60,
065003, 1999.
In this paper we studied the anomalous relaxation of scalar fluctuations in
high temperature scalar QED,as a model for understanding the infrared
singularities involved in the computation of the fermion damping rate.
Consistently with previous work in the literature, [5] we show
that the relaxation is non-exponential. The new point is that
the infrared divergences are managed by using the Dynamical
Renormalization Group approach (DRG). The DRG is a general method
of solution for differential equations (initial value problems)
which consists in a resummation of the secular terms appearing in
the naive perturbative solution, and it is valid even for
asymptotically large times. The same method has been successfully
applied in a variety of situations [6].
- [CSD]
Relaxing near the critical point, D. Boyanovsky, H. J. De
Vega, M. Simionato, LPTHE-00-16, hep-ph/0004159 , 41pp. Published
in Phys. Rev. D63:045007, 2001.
Here we studied the thermalization rate for critical systems. By
considering a scalar
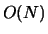 model at the critical temperature and
working non-perturbatively at next-to-leading order in the large
model at the critical temperature and
working non-perturbatively at next-to-leading order in the large 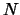 expansion, we found a critical slowing down behavior for long
wavelengths. This means that the time needed to thermalize long
wavelengths fluctuations (i.e. homogenous field configurations)
increases up to infinity. This fact has phenomenological
consequences, since it means that near a second order phase
transition one should expect sensible deviation from equilibrium
for the distribution functions of soft particles.
expansion, we found a critical slowing down behavior for long
wavelengths. This means that the time needed to thermalize long
wavelengths fluctuations (i.e. homogenous field configurations)
increases up to infinity. This fact has phenomenological
consequences, since it means that near a second order phase
transition one should expect sensible deviation from equilibrium
for the distribution functions of soft particles.
- [LP]The Landau Pole at Finite Temperature, H. J. de
Vega and M. Simionato, hep-ph/0011268, 6 pp. Published in Phys.
Rev. D64: 021703, 2001.
This paper differs from the others since it addresses a purely
equilibrium issue, i.e. how the position of the ultraviolet Landau
pole changes for a trivial theory when the existence of a medium
at temperature
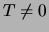 is taken in account. We found analytically
in the case of the
is taken in account. We found analytically
in the case of the 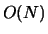 linear sigma model that the Landau pole position
increases with the temperature, i.e. the range of validity of the
theory increases when there are in-medium effects. As a
consequence the theory behaves perfectly well even at temperatures
well beyond the zero-temperature Landau pole (which I remind can
be at low energies for strongly coupled theories, like for
instance the pion
linear sigma model that the Landau pole position
increases with the temperature, i.e. the range of validity of the
theory increases when there are in-medium effects. As a
consequence the theory behaves perfectly well even at temperatures
well beyond the zero-temperature Landau pole (which I remind can
be at low energies for strongly coupled theories, like for
instance the pion 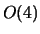 model).
model).



Next: Activity on Wilson Renormalization
Up: Scientific Activity
Previous: Activity on Non-Equilibrium Quantum
Michele Simionato
2003-03-07