An important reason for the public's concern about nuclear power is an unjustifiable fear of the hazards from radioactive waste. Even people whom I know to be intelligent and knowledgeable about energy issues have told me that their principal reservation about use of nuclear power is the disposal of radioactive waste. Often called an unsolved problem, many consider it to be the Achilles' heel of nuclear power. Several states have laws prohibiting construction of nuclear power plants until the waste disposal issue is settled. Yet ironically, there is general agreement among the scientists involved with waste management that radioactive waste disposal is a rather trivial technical problem. Having studied this problem as one of my principal research specialties over the past 15 years, I am thoroughly convinced that radioactive waste from nuclear power operations represents less of a health hazard than waste from any other large technological industry. Clearly there is a long and complex story to tell.
A FIRST PERSPECTIVE
What is this material that is so controversial? As we know from elementary physical science courses, matter can be neither created nor destroyed. When fuel is burned to liberate energy, the fuel doesn't simply disappear. It is converted into another form, which we refer to as "waste." This is true whether we burn uranium or coal or anything else. For nuclear fuels, this residue, called "high-level waste," has been the principal source of concern to the public.
As an initial perspective, it is interesting to compare nuclear waste with the analogous waste from a single large coal-burning power plant. The largest component of the coal-burning waste is carbon dioxide gas, produced at a rate of 500 pounds every second, 15 tons every minute. It is not a particularly dangerous gas, but it is the principal contributor to the "greenhouse effect" discussed at some length in Chapter 3. The other wastes from coal burning were also discussed in Chapter 3, but let's review them briefly. First and probably foremost is sulfur dioxide, the principal cause of acid rain and perhaps the main source of air pollution's health effects, released at a rate of a ton every 5 minutes. Then there are nitrogen oxides, the second leading cause of acid rain and perhaps also of air pollution. Nitrogen oxides are best known as the principal pollutant from automobiles and are the reason why cars need expensive pollution control equipment which requires them to use lead-free gasoline; a single large coal-burning plant emits as much nitrogen oxide as 200,000 automobiles. The third major coal burning waste is particulates including smoke, another important culprit in the negative health effects of air pollution. Particulates are released at a rate of several pounds per second. And next comes the ash, the solid material produced at a rate of 1,000 pounds per minute, which is left behind to cause serious environmental problems and long-term damage to our health. Coal-burning plants also emit thousands of different organic compounds, many of which are known carcinogens. Each plant releases enough of these compounds to cause two or three cancer deaths per year.1 And then there are heavy metals like lead, cadmium, and many others that are known or suspected of causing cancer, plus a myriad of other health impacts. Finally there is uranium, thorium, and radium, radioactive wastes released from coal burning that serve as a source of radon gas. The impact of this radioactive radon gas from coal burning on the public's health far exceeds the effects of all the radioactive waste released from nuclear plants (see Chapter 12).
The waste produced from a nuclear plant is different from coal-burning wastes in two very spectacular ways. The first is in the quantities involved: the nuclear waste is 5 million times smaller by weight and billions of times smaller by volume. The nuclear waste from 1 year of operation weighs about 1½ tons2 and would occupy a volume of half a cubic yard, which means that it would fit under an ordinary card table with room to spare. Since the quantity is so small, it can be handled with a care and sophistication that is completely out of the question for the millions of tons of waste spewed out annually from our analogous coal-burning plant.
The second pronounced difference is that the nuclear wastes are radioactive, providing a health threat by the radiation they emit, whereas the principal dangers to health from coal wastes arise from their chemical activity. This does not mean that the nuclear wastes are more hazardous; on nearly any comparison basis the opposite is true. For example, if all the air pollution emitted from a coal plant in one day were inhaled by people, 1½ million people could die from it,3 which is 10 times the number that could be killed by ingesting or inhaling the waste produced in one day by a nuclear plant.4
This is obviously an unrealistic comparison since there is no way in which all of either waste could get into people. A more realistic comparison might be on the basis of simple, cheap, and easy disposal techniques. For coal burning this would be to use no air pollution control measures and simply release the wastes without inhibition. This is not much worse than what we are doing now since the smoke abatement techniques, which are the principal pollution control on most coal-burning plants, contribute little to health protection. We have seen in Chapter 3 that air pollution causes about 75 deaths per year from each plant. Some other comparably serious consequences will be considered later in this chapter.
For nuclear waste, a simple, quick, and easy disposal method would be to convert the waste into a glass — a technology that is well in hand — and simply drop it into the ocean at random locations.5 No one can claim that we don't know how to do that! With this disposal, the waste produced by one power plant in one year would eventually cause an average total of 0.6 fatalities, spread out over many millions of years, by contaminating seafood. Incidentally, this disposal technique would do no harm to ocean ecology. In fact, if all the world's electricity were produced by nuclear power and all the waste generated for the next hundred years were dumped in the ocean, the radiation dose to sea animals would never be increased by as much as 1% above its present level from natural radioactivity.
We thus see that if we compare the nuclear and coal wastes on the basis of cheap, simple, and easy disposal techniques, the coal wastes are (7.5 / 0.06 =) 120 times more harmful to human health than nuclear waste. This treatment ignores some of the long-term health effects of coal burning to be discussed later.
Another, and very different, way of comparing the dangers of nuclear and coal waste is on the basis of how much they are changing our exposures to toxic agents. The typical level of sulfur dioxide in the air of American cities is 10 times higher than natural levels, and the same is true for the principal nitrogen oxides.6 For cancer-causing chemicals the ratio is much higher.7 These are matters that might be of considerable concern in view of the fact that we really do not understand the health effects of these agents very well. For radioactive waste from a flourishing nuclear industry, on the other hand, radiation exposures would be increased by only a tiny fraction of 1% above natural levels.8
Another basis for comparison between the wastes from nuclear and coal burning is the "margin of safety," or how close average exposure is to the point where there is direct evidence for harm to human health. There have been several air pollution episodes in which there were hundreds of excess deaths, with sulfur dioxide levels about 1,000 micrograms per cubic meter,1 whereas levels around 100 micrograms per cubic meter, just 10 times less, are quite common in American cities. For radiation, on the other hand, exposures expected from hypothetical problems with nuclear waste are in the range of 1 mrem or less, tens of thousands of times below those for which there is direct evidence for harm to human health.
All of these comparisons have been intended as an introduction to the subject. Now, let us look into the problem in some detail.
HIGH-LEVEL RADIOACTIVE WASTE
The fuel for a nuclear reactor is in the form of ceramic pellets of uranium oxide, each about ½ inch in diameter and 3/4 inch long, lined up and sealed inside metal tubes about 12 feet long and ½ inch in diameter. About 50 of these "fuel pins" are bound together, leaving space for water to circulate between the pins, to form a "fuel assembly." A large reactor might contain 200 of these fuel assemblies arranged in a lattice, with a total of 110 tons of uranium. A typical fuel assembly remains in the reactor for about 3 years. During this time, a small percentage of the uranium nuclei are struck by neutrons, causing them to undergo fission or other nuclear reactions. These reactions transform them into other nuclei, "the high-level radioactive waste." At the end of this 3-year period, the fuel is "spent" and must be replaced by fresh fuel. The subject we examine here is disposal of this spent fuel containing the radioactive waste.
One option is to dispose of the spent fuel directly by sealing fuel assemblies into canisters and burying them. A much more rational approach from the standpoint of long-range planning is to put the fuel through a chemical reprocessing operation to separate out the uranium and plutonium which are valuable for future use as fuels, and to convert the residual material into a form suitable for burial. If we follow the first option, our uranium resources will run out sometime during the next century, whereas the second option can provide all of the energy humans will need for as long as they inhabit planet Earth, without an increase in fuel costs (see Chapter 13).
Unfortunately, decisions are not made by long-range planners, but rather by business executives and politicians who base their decisions on short-term economics. Even from this standpoint, reprocessing is the more favorable option, albeit by a rather narrow margin. Consequently, reprocessing plants have been an important part of nuclear industry planning in the United States. In the late 1960s and early 1970s, three commercial plants were built, one of them was operated for a few years, and still other plants reached the advanced planning stage. However, the opposition to nuclear power in the late 1970s caused severe setbacks for the reprocessing industry, leading to its demise (see Chapter 13). Therefore, current U.S. plans are to bury the spent fuel directly.
The situation is very different in other countries. Great Britain has been reprocessing spent fuel since the 1950s and is currently constructing a large new plant. France has been operating two reprocessing plants for many years and its third plant is nearly complete. Germany has been operating a small reprocessing plant since 1971, and a much larger one is under construction with a 1996 start-up date. Japan has a small plant in operation; a much larger one, under construction, is scheduled to come on line in 1995. The Japanese also send some spent fuel to France and Great Britain for reprocessing. Belgium, Italy, Switzerland, and the Netherlands also utilize the French and British facilities. India has one reprocessing plant in operation and has recently begun construction of another. China, where nuclear power is in its infancy, is planning to operate a pilot plant by 1995 and a full-scale unit by 2010. The Soviet Union reprocesses its spent fuel, and Eastern bloc countries as well as Finland make use of the Soviet facilities. Sweden, Canada, and Spain are providing for long-term storage of spent fuel, and are therefore deferring a decision on reprocessing.
Only the United States has a full-scale program in operation leading to burial of spent fuel, although it would be very easy to change it to include reprocessing. This option will remain open for a long time, since even after burial the spent fuel will be retrievable for several decades.
While I fully understand the basis for the U.S. policy of burying spent fuel and I support it, I cannot believe that it will persist for more than 20 years or so. I therefore base the risk evaluations on the assumption that we will eventually do reprocessing. If I am wrong on this matter and spent fuel is permanently buried, the risks we will be discussing will be increased about 10-fold. Nevertheless it will be evident that this would not appreciably affect the conclusions of our discussion.
HAZARDS AND PROTECTIVE BARRIERS
Probably the most frequent question I receive about nuclear power is, "What are we going to do with the radioactive waste?" The answer is very simple: we are going to convert it into rocks and put it in the natural habitat for rocks, deep underground. The next question is usually, "How do you know that will be safe?" Answering that question is our next topic for consideration.
This discussion will be in terms of the high-level waste produced by one large power plant (1,000,000 kW) in one year. The high-level waste from such a plant is contained inside the fuel. If we are to have reprocessing, the 35 tons of spent fuel will be shipped to a chemical reprocessing plant where it will be dissolved in acid and put through chemical processes to remove 99.5% of the uranium and plutonium that are valuable as fuels for future use. The residue — 1.5 tons of high-level waste — will then be incorporated into a glass in the form of perhaps 30 cylinders, each about 12 inches in diameter and 10 feet long, weighing about 1,000 pounds. There is a great deal of research on materials that may be superior to glass as a waste form, but far more is now known about glass, a material whose fabrication is simple and well developed. There is no evidence that it is not satisfactory. Many natural rocks are glasses, and they are as durable as other rocks.*
This 15 tons of waste glass, roughly one truckload, will then be shipped to a federal repository, where it will be permanently emplaced deep underground. The U.S. Department of Energy is now spending over $200 million per year in developing this waste storage technology. The program is paid for by a tax on nuclear electricity; about $6 billion was collected by the end of 1989. The estimated cost of handling and storing our one truckload of waste is $5 million, which corresponds to 0.07 cents per kilowatt-hour, about l% of the cost of electricity to the consumer.
I have often been told, "We don't want a waste dumping ground in our area." This conjures up a picture of dump trucks driving up and tilting back to allow their loads of waste to slide down into a hole in the ground. Clearly it doesn't cost $5 million for each truckload to do this, especially on a mass-handling basis. What is planned, rather, is a carefully researched and elaborately engineered emplacement deep underground in a mined cavity.
It may be of incidental interest to point out that the present $5 million price tag on storing one year's waste from one plant is several hundred times higher than the cost of the original plan as formulated in the 1960s. Those conversant with the earlier plan are still convinced that it provided adequate safety, although the added expenditures do, of course, contribute further safety. This tremendous escalation in the scope of the project is a tribute to the power of public hysteria in a democracy like ours, whether or not that hysteria is justified. It is also an application of Parkinson's Law — it was clearly acceptable to devote 1% of the cost of electricity to disposal of the waste, so the money was "available," and being available, the government has found ways to use it.
There have been many safety analyses of waste repositories,9 and all of them agree that the principal hazard is that somehow the waste will be contacted by groundwater, dissolved, and carried by the groundwater into wells, rivers, and soil. This would cause contamination of drinking water supplies or, through pick-up by plant roots, contamination of food. It could thereby get into human stomachs.
The chance of this waste becoming suspended in air as a dust and inhaled by humans is very much less because groundwater rarely reaches the surface; moreover, we inhale only about 0.001 grams of dust per day (and 95% of this is filtered out by hairs in the nose, pharynx, trachea, and bronchi and removed by mucous flow), whereas we eat over 1,000 grams of food per day. On an average, an atom in the top inch of U.S. soil has 1 chance in l0 billion per year of being suspended as a dust and inhaled by a person, whereas an atom in a river, into which groundwater normally would bring the dissolved waste, has 1 chance in l0 thousand of entering a human stomach.10 Thus, an atom of waste has a much better chance of becoming absorbed into the body with food or water than with inhaled dust.
External irradiation by radioactive materials in the ground is also a lesser problem. Rock and soil are excellent shielding materials; while the waste remains buried, not a single particle of radiation from it can ever reach the surface (See Chapter 11 Appendix). Compare this with the 15,000 particles of radiation from natural sources that strike each of us every second. If radioactivity is released by groundwater, this shielding is still effective as long as it remains underground or dissolved in river water. If the radioactivity does somehow become deposited on the ground surface, it will soon be washed away or into the ground by rain. The great majority of the radiation is absorbed by building materials, clothing, or even the air. Thus, there would be relatively little exposure to the human body due to radiation originating from materials on the ground.
Quantitative calculations confirm that food and water intake is the most important mode of exposure from radioactive waste, a position agreed upon in all safety analyses.9 Hence we will limit our consideration to that pathway. In order to estimate the hazard, we therefore start by determining the cancer risk from eating or drinking the various radioactive materials in the waste.
 |
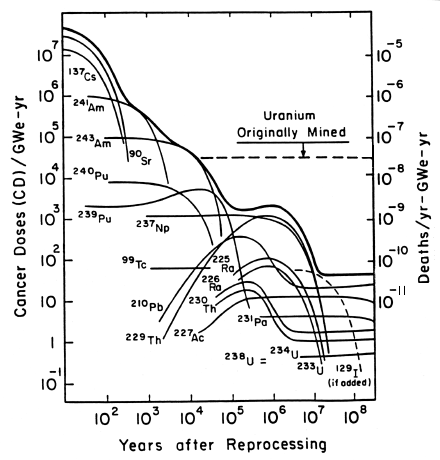
| Fig. 1 — Toxicity of high-level radioactive waste versus time.8 The ordinate is the number of cancer deaths that would be expected if all the waste prouced by one large nuclear power plan in one year were eaten by people. The individual curves show the toxicity of the individual radioactive species in the waste (as labeled), and the top black curve shows their sum, the total toxicity. The horizontal dashed line shows the number of deaths expected if the uranium mined out of the ground to produce the fuel from which this waste was generated were fed to people. The scale on the right shows the deaths per year expected according to the risk analysis. |
The method for calculating this is explained in the Chapter 11 Appendix, but the results8 are shown in Fig. 1. For present purposes we need only look at the thick line which is above all the others in the figures. This is a plot of the number of cancers that would be expected if all of the waste produced by one plant in one year were fed to people.
If this were done shortly after burial, according to Fig. 1 we would expect 50 million cancers, whereas if it were done after 1,000 years there would be 300,000, and if after a million years there would be 2,000. Note that we did not specify how many people are involved because that does not matter.*
If nuclear power was used to the fullest practical extent in the United States, we would need about 300 power plants of the type now in use. The waste produced each year would then be enough to kill (300 x 50 million =) over 10 billion people. I have authored over 250 scientific papers over the past 35 years presenting tens of thousands of pieces of data, but that "over lO billion" number is the one most frequently quoted. Rarely quoted, however, are the other numbers given along with it11: we produce enough chlorine gas each year to kill 400 trillion people, enough phosgene to kill 20 trillion, enough ammonia and hydrogen cyanide to kill 6 trillion with each, enough barium to kill 100 billion, and enough arsenic trioxide to kill 10 billion. All of these numbers are calculated, as for the radioactive waste, on the assumption that all of it gets into people. I hope these comparisons dissolve the fear that, in generating nuclear electricity, we are producing unprecedented quantities of toxic materials.
One immediate application of Fig. 1 is to estimate how much of the waste glass, converted into digestible form, would have a good chance of killing a person who eats it — this may be called a "lethal dose." We calculate it by simply dividing the quantity of waste glass, l5 tons, by the values given by the curve in Fig. 1, and the results are as follows:
| Shortly after burial | 0.01 oz. | |
| After 100 years | 0.1 oz. | |
| After 600 years | 1 oz. | |
| After 20,000 years | 1 lb. |
Lethal doses for some common chemicals are as follows11:
| selenium compounds | 0.01 oz. | |
| potassium cyanide | 0.02 oz. | |
| arsenic trioxide | 0.1 oz. | |
| copper | 0.7 oz. |
Note that the nuclear waste becomes less toxic with time because radioactive materials decay, leaving a harmless residue, but the chemicals listed retain their toxicity forever.
By comparing these two lists we see that radioactive waste is not infinitely toxic, and in fact it is no more toxic than some chemicals in common use. Arsenic trioxide, for example, used as an herbicide and insecticide, is scattered on the ground in regions where food is grown, or sprayed on fruits and vegetables. It also occurs as a natural mineral in the ground, as do other poisonous chemicals for which a lethal dose is less than one ounce.
Since the waste loses 99% of its toxicity after 600 years, it is often said that our principal concern should be limited to the short term, the first few hundred years. Some people panic over the requirement of security even for hundreds of years. They point out that very few of the structures we build can be counted on to last that long, and that our political, economic, and social structures may be completely revolutionized within that time period. The fallacy in that reasoning is that it refers to our environment here on the surface of the earth, where it is certainly true that most things don't last for hundreds of years. However, if you were a rock 2,000 feet below the surface, you would find the environment to be very different. If all the rocks under the United States more than 1,000 feet deep were to have a newspaper, it couldn't come out more than once in a million years, because there would be no news to report. Rocks at that depth typically last many tens of millions of years without anything eventful occurring. They may on rare occasions be shaken around or even cracked by earthquakes or other catastrophic events, but this doesn't change their position or the chemical interaction with their surroundings.
One way to comprehend the very long-term toxicity in the waste is to compare it with the natural radioactivity in the ground. The ground is, and always has been, full of naturally radioactive materials — principally potassium, uranium, and thorium. On a long-term basis (thousands of years or more), burying our radioactive waste would increase the total radioactivity in the top 2,000 feet of U.S. rock and soil only by 1 part in 10 million. Of course, the radioactivity is more concentrated in a waste repository, but that doesn't matter. The number of cancers depends only on the total number of radioactive atoms that get into people, and there is no reason why this should be larger if the waste is concentrated than if it is spread out all over the country. In fact, quite the opposite is the case: being concentrated in a carefully selected site deep underground with the benefit of several engineered safeguards and subject to regular surveillance provides a given atom far less chance of getting into a human stomach than if it is randomly located in the ground. Incidentally, it can be shown that the natural radioactivity deep underground is doing virtually no damage to human health, so adding a tiny amount to it is essentially innocuous.
When I point out that concentration of the waste in one place does not increase the health hazard, listeners often comment that it does mean that the risks will be concentrated on the relatively small number of people who live in that area. That, of course, is true, but it is also true for just about any other environmental problem. We in Pittsburgh suffer from the air pollution generated in making steel for the whole country; citizens of Houston and a few other cities bear the brunt of the considerable health hazards from oil refineries that make our gasoline, and there are any number of similar examples. The health burden from these inequities is thousands of times larger than those from living near a nuclear waste repository will ever be.
Fig. 1 shows the toxicity of the uranium ore that was originally mined out of the ground to produce the fuel from which the waste was generated. Note that it is larger than the toxicity of the waste after 15,000 years; after that the hazard from the buried waste is less than that from the ore if it had never been mined. After 100,000 years, there is more radioactive toxicity in the ground directly above the repository (i.e., between the buried waste and the surface) than in the repository itself due to the natural radioactivity in the rock.
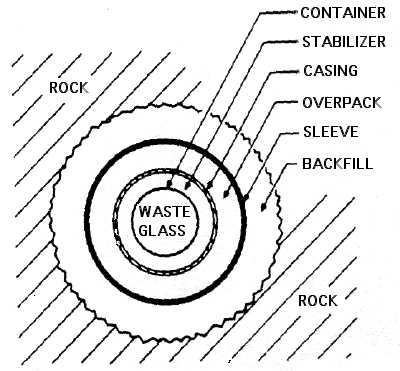 |
| Fig. 2 — Schematic diagram of buried waste package. Components are as follows: waste glass - the waste itself, converted into a glass; container - stanless steel can in which glass is originally cast; stabilizer - filler material to improve physical and chemical stability of the waste; casing - special material highly resistant to corrosion by intruding water, which it should keep out; overpack - provides additional corrosion resistance and structural stability; sleeve - liner for hole, gives structural support; backfill - material to fill space between waste package and rock, swells when wet to keep water out; if waste becomes dissolved, backfill absorbs it out of the escaping water. |
A schematic diagram of the waste package, as buried, is shown in Fig. 2. It is enlightening to consider the protections built into the system to mitigate the hazards. For the first few hundred years, when the toxicity is rather high, there is a great deal of protection through various time delays before the waste can escape through groundwater. First and foremost, the waste will be buried in a rock formation in which there is little or no groundwater flow, and in which geologists are as certain as possible that there will be little groundwater flow for a very long time. If the geologists are wrong and an appreciable amount of water flow does develop in the rock formation in which the waste is buried, it would first have to dissolve away large fractions of that rock — roughly half of the rock would have to be dissolved before half of the waste is dissolved. This factor might seem to offer minimal protection if the waste is buried in salt, since salt is readily dissolved in water. However, in the New Mexico area, where a repository for defense waste has been constructed, if all the water now flowing through the ground were diverted to flow through the salt, it would take a million years to dissolve the salt enclosing a repository.11 The quantity of salt is enormous, while the water flow is not a stream but more like a dampness, slowly progressing through the ground.
The next layer of protection is the backfill material surrounding the waste package (see Fig. 2). This will be a clay, which tends to swell when wet to form a tight seal keeping water flow away from the package.
If water should penetrate the backfill, before it can reach the waste it must get past the metal casing in which the waste glass is to be sealed. Materials for this casing have been developed that give very impressive resistance to corrosion. One favorite is a titanium alloy, which was tested in a very hot (480°F versus a maximum expected repository temperature of 250°F) and abnormally corrosive solution, and even under these extreme conditions, corrosion rates were such that water penetration would be delayed for a thousand years.12 Under more normal groundwater conditions, these casings would retain their integrity for hundreds of thousands of years. Thus, the casings alone provide a rather complete protection system even if everything else fails.
The next layer of protection is the waste form, probably glass, which is not readily dissolved. Glass artifacts from ancient Babylonia have been found in river beds, where they have been washed over by flowing river water — not just by the slowly seeping dampness which better describes groundwater conditions — for 3,000 years without dissolving away.13 A Canadian experiment with waste glass buried in soil permeated by groundwater indicates that it will last for a hundred million years — i.e., only about 1/100 millionth dissolves each year.
But suppose that somehow some of the waste did become dissolved in groundwater. Groundwater moves very slowly, typically at less than 1 foot per day — in the region of the New Mexico site it moves only about 1 inch per day and at the Nevada site which is under investigation it moves only 0.03 inches per day. Furthermore, groundwater deep underground does not ordinarily travel vertically upward toward the surface; it rather follows the rock layers, which tend to be essentially horizontal, and hence it typically must travel about 50 miles before reaching the surface. In the New Mexico area it must travel over a hundred miles and at the Nevada site at least 30 miles. Anyone can easily calculate that to travel 50 miles at 1 foot per day takes about 1,000 years, so this again gives a very substantial protection for the few hundred years that most concern us here. (Long-term effects will be considered later.)
But the radioactive material does not move with the velocity of the groundwater. It is constantly filtered out by adsorption on the rock material, and as a result it travels hundreds or thousands of times more slowly than the groundwater.14 If the groundwater takes a thousand years to reach the surface, the radioactive materials should take hundreds of thousands or millions of years. Moreover, there are abundant opportunities along the way for waste materials to precipitate out of solution and become a permanent part of the rock.15
We thus have seven layers of protection preventing the waste from getting out during the first few hundred years when it is highly toxic: (l) the absence of groundwater, (2) the insolubility of the surrounding rock, (3) the sealing action of the backfill material, (4) the corrosion resistance of the metal casing, (5) the insolubility of the waste glass itself, (6) the long time required for groundwater to reach the surface, and (7) the filtering action of the rock. But even if all of these protections should fail, the increased radioactivity in the water would be easily detected by routine monitoring, and the water would not be used for drinking or irrigation of food crops; thus there would still be no damage to human health.
QUANTITATIVE RISK ASSESSMENT FOR HIGH-LEVEL WASTE
Our next task is to develop a quantitative estimate of the hazard from buried radioactive waste.8 Our treatment is based on an analogy between buried radioactive waste and average rock submerged in groundwater. We will justify this analogy later, but it is very useful because we know a great deal about the behavior of average rock and its interaction with groundwater. Using this information in a calculation outlined in the Chapter 11 Appendix demonstrates that an atom of average rock submerged in groundwater has one chance in a trillion each year of being dissolved out of the rock, eventually being carried into a river, and ending up in a human stomach.
In the spirit of our analogy between this average rock and buried radioactive waste, we assume that this probability also applies to the latter; that is, an atom of buried radioactive waste has one chance in a trillion of reaching a human stomach each year. The remainder of our calculation is easy, because we know from Fig. 1 the consequences of this waste reaching a human stomach. All we need do is multiply the curve in Fig. 1 by one-trillionth to obtain the number of fatal cancers expected each year. This is done by simply relabeling the vertical scale, as shown on the right side of Fig. 1. For example, if all of the waste were to reach human stomachs a thousand years after burial, there would be 300,000 deaths, according to the scale on the left side of Fig. 1, but since only one-trillionth of it reaches human stomachs each year, there would be (300,000 / 1 trillion =) 3 X 10-7 deaths per year, as indicated by reading the curve with the scale on the right side of Fig. 1. This result is equivalent to one chance in 3 million of a single death each year.
What we really want to know is the total number of people who will eventually die from the waste. Since we know how many will die each year, we simply must add these up. Totalling them over millions of years gives 0.014 eventual deaths. One might ask how far into the future we should carry this addition, and therein lies a complication that requires some explanation.
From the measured rate at which rivers carry dissolved and suspended material into the ocean each year, it is straightforward to calculate that the surfaces of the continents are eroding away at an average rate of 1 meter (3.3 feet) of depth every 22,000 years. (All the while the continents are being uplifted such that on an average the surface remains at about the same elevation.) Nearly all of this erosion comes from river beds and the minor streams and runoff that feed them. However, rivers change their courses frequently; changing climates develop new rivers and eliminate old ones (e.g., 10,000 years ago the Arizona desert was a rain forest); and land areas rise and fall under geological pressures to change drainage patterns. Therefore, averaged over very long time periods, it is reasonable to assume that most land areas erode away at roughly this average rate, 1 meter of depth every 22,000 years. This suggests that the ground surface will eventually erode down to the level of the buried radioactive waste. Since the waste will be buried at a depth of about 600 meters, this may be expected to occur after about (600 x 22,000 =) 13 million years. When it happens, the remaining radioactivity will be released into rivers, and according to estimates developed in the Chapter 11 Appendix, one part in 10,000 will get into human stomachs.
Therefore, the process of adding up the number of deaths each year should be discontinued after 13 million years; that was done in calculating the number of deaths given above as 0.014. To this we must add the number of deaths caused by release of the remaining radioactivity. A simple calculation given in the Chapter 11 Appendix shows that this leads to 0.004 deaths. Adding that number to the 0.014 deaths during the first l3 million years gives 0.018 as the total number of eventual deaths from the waste produced by one power plant in one year. This is the final result of this section, 0.018 eventual fatalities. Recall now that air pollution, one of the wastes from coal burning, kills 75 people in generating the same amount of electricity; perhaps new pollution control technology may reduce this number to 15 deaths per year. Even if this comes to pass, we see that this one waste from coal burning would still be a thousand times more injurious to human health than are the high-level nuclear wastes.
Another way of understanding the results of our analysis is to consider a situation in which all of the present electricity used in the United States has been provided by nuclear power plants — about 300 would be required — continuously for millions of years. We would then expect (300 x 0.018 =) 5.4 cancer deaths per year on an average from all of the accumulated waste. Compare this with the 30,000 deaths each year we now get from coal-burning power plants.
Before closing this section, readers with a scientific bent may be interested in the justification for the basic assumption used in arriving at our estimate, the analogy between buried radioactive waste and average rock which is submerged in flowing groundwater. Actually, there are three ways in which the waste may be less secure:
Since we have discussed the three ways in which buried waste may be less secure than the average rock used in our analogy, it is appropriate to point out ways in which it is more secure. In the first place, burial will be in an area free of groundwater flow, whereas the rock we considered was already submerged in flowing groundwater. Second, it will be in a carefully chosen rock environment, whereas the rock in our analogy is in an average environment; it might, for instance, be in an area of extensive rock fracturing. Third, the waste package will be in a special casing which provides extreme resistance to water intrusion, a protection not available to average rock; this casing should provide adequate protection even if everything else imaginable goes wrong. And finally, if any radioactive waste should escape and get into food and water supplies, it would very probably be detected by routine monitoring programs in plenty of time to avert any appreciable health consequences.
In balancing the ways in which buried waste is more secure and less secure than the average rock submerged in groundwater with which we compared it, it seems reasonable to conclude that our analogy is a fair one. If anything, it overestimates the dangers from the waste.
It should be pointed out that there are other methods than the one presented here for quantifying the probability for an atom of material in the ground to enter a human stomach. For example, we know the amounts of uranium and radium in the human body from measurements on cadavers, and we know the amounts in the ground. From the ratios of these, we can estimate the probability per year for an atom of these elements in the ground to enter a human body. This gives a result in good agreement with that of the calculation we presented.
Sometimes when I complete a demonstration like the one above of the safety of buried radioactive waste, a listener complains that the demonstration is invalid because we don't know how to bury waste. How anyone can possibly be so naive as to believe that we don't know how to bury a simple package is truly a challenge to my imagination. Many animals bury things, and people have been burying things for millions of years. Any normal person could easily suggest several different ways of burying a waste package. Why, then, are we devoting so much time and effort to developing a waste burial technology? The problem here is to decide on the best way of burying the waste to maximize its security. Whether it is worthwhile to go to such pains to optimize the solution is highly questionable, especially since we have shown that even the haphazard burial of average rock by natural processes would provide adequate safety. But the public's irrational worries about the dangers have forced our government to spend large sums of money on the problem. Actually, we are paying for it in our electricity bills. Fortunately, it only increases our bills by one percent.
LONG-TERM WASTE PROBLEMS FROM CHEMICAL CARCINOGENS
In order to appreciate the meaning of the result obtained in the last section — 0.018 eventual cancer deaths from each plant-year of operation — it is useful to put it in perspective by comparing it with the very long-term cancer risks from the buried wastes produced by other methods of generating electricity. Here we consider certain types of chemicals that cause cancer8; other examples will be given in the next chapter.
The only reason buried radioactive waste has a calculable health effect is because we are using a linear dose-response relationship, assuming, for example, that if 1 million mrem causes a given risk, 1 mrem will cause a millionth of that risk. This linear relationship does not apply to most toxic chemicals, like carbon monoxide poisoning, for which there is a "threshold" exposure required before there can be any harm. However, it is now widely believed that a linear, no-threshold relationship is valid for chemical carcinogens (i.e., chemicals that can induce cancer) just as for radiation. Basically, the reason for this thinking in both cases is that cancer starts from injury to a single molecule on a single chromosome in the nucleus of a single cell, often induced by a single particle of radiation or by a single carcinogenic molecule. The probability for this simple process is not dependent on whether or not other carcinogenic molecules are causing injury elsewhere. Thus the probability of cancer is simply proportional to the number of carcinogenic molecules taken into the body, as described by a linear relationship. This linear, no-threshold, dose-response relationship for chemical carcinogens has now been officially accepted by all U.S. Government agencies charged with responsibilities in protecting public health, such as the Environmental Protection Agency, the Occupational Safety and Health Administration, and the Food and Drug Administration.
The particular carcinogens of interest in our discussion are the chemical elements cadmium, arsenic, beryllium, nickel, and chromium. There is a considerable body of information indicating that all of these cause cancer and enough quantitative information to estimate the risk per gram of intake. All of them are present in small amounts in coal. Therefore, when coal is burned, they are released and eventually, by one route or another, end up in the ground. Small amounts of each of them are also contained in food. All such materials in food, of course, are taken in from the ground through the roots of plants.
As in the case of radioactive waste, the principal problem in evaluating the hazard is to estimate the probability for an atom of these elements in the ground eventually to reach a human stomach. However, the problem is simpler here because the toxicity in these carcinogenic elements does not decay with time, as does that of radioactive waste. Since some quantity of these elements is ingested by humans every year, if an atom remains in the ground indefinitely, eventually after a long enough time, it has a good chance of reaching a human stomach. However, there are other processes for removing materials from the ground. The most important of these is erosion of soil, with the materials being carried by rivers into the oceans. The probability for an atom in the ground to enter a human stomach is therefore the probability for this to happen before it is washed into the oceans. This is just the ratio of the rate for entering human stomachs to the rate of removal by erosion.
The rates for both of these are known. From chemical analyses of food and the quantity consumed each year, we can calculate the rate at which cadmium, for example, enters human stomachs in the United States. From the rate at which American soil is washed into oceans and the measured abundance of cadmium in soil, we can calculate the rate at which cadmium is carried into oceans. We thus can determine the probability for an atom of cadmium in the soil to enter a human stomach. It turns out to be surprisingly high, about 1.3%. It is 5 times smaller for arsenic, 20 times lower for beryllium and nickel, and 60 times lower for chromium (cadmium atoms are more easily picked up by plant roots because of their chemical properties).
Since we know the quantities of each of these carcinogenic elements deposited into the top layers of the ground as a result of coal burning, the probability for them to be transferred from the ground into humans, and their cancer risk once ingested, it is straightforward to estimate the number of deaths caused by coal burning. The result is about 50 deaths due to one year's releases from one large plant. These deaths are spread over the time period during which the top few meters of ground will be eroded away, about l00,000 years.*
If one takes a much longer-term viewpoint, these deaths would have eventually occurred even if the coal had not been mined and burned, because after several millions of years, erosion would have brought this coal near the surface, where its cadmium, arsenic, beryllium, chromium, and nickel could have been picked up by plant roots and gotten into food.
However, the fact that the coal was mined means that its turn near the surface is taken by other rock which, we assume, has the average amount of these carcinogenic elements in it. This carcinogenic material represents a net additional health risk to humankind due to the use of coal. Taking this into account, the final result is that there would be a net excess of 70 deaths. Note that this is thousands of times larger than the 0.018 deaths from high-level radioactive waste.
The chemical carcinogens also have an impact on the long term health consequences of electricity produced by solar energy. We have already pointed out that producing the materials for deployment of a solar array requires about 3% as much coal burning as producing the same amount of electricity by direct coal burning. The quantity of chemical carcinogens released in the former process is therefore 3% of those released in the latter, so in the very long term we may expect about 2 eventual deaths (3% of 70) from an amount of solar electricity equivalent to that produced by a large nuclear or coal-fired power plant in one year. This is a small number, but it is still a hundred times the 0.018 deaths from nuclear plant waste.
But there may be much more important problems. A prime- candidate material for future solar cells is cadmium sulfide. When these cells deteriorate, that material will probably be disposed of in one way or another into the ground. The cadmium introduced into the ground in this way is estimated to eventually cause, 80 deaths for the quantity of electricity produced by a large nuclear plant in one year. Most of the cadmium used in this country is imported. Thus, in contrast to the situation for coal, it would not have eventually reached the surface of U.S. soil without this technology. Again we encounter consequences thousands of times higher than the 0.018 deaths from radioactive waste.
SHOULD WE ADD UP EFFECTS OVER MILLIONS OF YEARS?
Many may be bothered by the idea of adding up effects over millions of years as we have been doing in this chapter. Personally, I agree with them. The idea of considering effects over such long time periods was introduced by opponents of nuclear power, who often insist that it be done. The analyses presented above show that such a procedure turns out very favorably for nuclear power. However, there are many good reasons for confining our attention to the "foreseeable future," which is generally interpreted to be l00-l,000 years. Several groups, including most government agencies, have adopted 500 years as a reasonable time period for consideration, so we will use it for this discussion.
The reason for ignoring lives that may be lost in the far future is not because those lives are less valuable than our own or those of our closer progeny. There surely can be no moral basis for any such claim. But there are at least three reasonable and moral bases for ignoring the distant future.16
One such basis is the improvement in cancer-cure rates. In recent years, they have been improving by about 0.5% per year. It is unlikely that cure rates will continue to improve at this rate. More probably they will stagnate before long, or on the other hand there may be a breakthrough leading to a dramatic improvement. But most knowledgeable people agree that there is a good chance that cancer will be a largely curable disease in 500 years. The deaths we calculate to occur after that time will therefore probably never materialize.
The second basis for ignoring deaths calculated to occur in the distant future is what I call the "trust fund" approach. We showed in Chapter 8 that there are many ways that money can be used to save lives at a rate of at least one life saved per $100,000 spent. But even suppose that so many improvements are instigated that it will cost $1 million to save a life in the distant future (all our discussions discount inflation). There is a continuous record extending back 5,000 years of money always being able to draw at least 3% real (i.e., discounting inflation) interest. Each dollar invested now at 3% interest is worth $2.5 million after 500 years and will therefore be capable of saving more than one life. It is therefore much more effective in saving far future lives to set up a trust fund to be spent in their time for that purpose rather than for us to spend money now to protect them from our waste. One might wonder about the mechanics and practicality of setting up a trust fund to be transmitted to future generations, but this is no problem. By overspending, we are now building up a public debt that they will have to pay interest on, so rather than actually set up a trust fund, we need only reduce our spending and thereby leave future generations with more money to use for lifesaving. By not spending profligately on waste management, we are doing just that.
A third basis for ignoring the distant future in our considerations is the "biomedical research" approach. If we don't feel comfortable with the "trust fund" approach of putting aside money to be spent in the future for saving lives, we can save future lives by spending money today on biomedical research. One study concludes that the $68 billion spent on such research between 1930 and 1975 is now saving 100,000 lives per year in the United States, one life per year for every $680,000 spent. Another study estimates that the $20 billion spent in 1955-1965 is now saving 100,000 lives per year, or one life per year for every $200,000 spent. Age-specific mortality rates in the United States have been declining steadily in recent years; if one-fourth of this decline is credited to biomedical research, the latter is now saving one life per year for every $1 million spent. As the easier medical problems are solved and the more difficult ones are attacked, the cost goes up. Let us therefore say that for the near future, it will cost $5 million to save one life per year in the United States, not to mention that it will save lives in other countries. Over the next 500 years, saving one life per year will avert a total of 500 deaths, a cost of $10,000 per life saved. If we extend our considerations beyond 500 years, the price drops proportionally. Since we are now spending many millions of dollars per future life saved in handling our radioactive waste, it would clearly be much more beneficial to future generations if we put this money into biomedical research.
The straightforward way to implement this alternative would be for the nuclear industry to contribute money to biomedical research rather than to improved long-term security of nuclear waste, but even that may not be necessary. The nuclear industry pays money to the government in taxes, and the government spends roughly an equal sum of money to support biomedical research. All that is necessary to implement an equitable program from the viewpoint of future citizens is that 0.1% of this cash flow from the nuclear industry to government to biomedical research be redefined as support of biomedical research by the nuclear industry. If it would make people happier, the government tax on the nuclear industry could actually be raised by 0.1% and this money could be directly added to the government's biomedical research budget. No one would notice the difference since it is much less than a typical annual change in these taxes and budgets.
As a result of any one of the above three rationales, or a combination of them, many people, including myself, feel that we should worry only about effects over the next 500 years. For their benefit we now develop estimates of the health effects expected during that time period, from one year's operation of a large power plant8:
For the high-level radioactive waste, we take the number of fatalities each year from using the scale on the right side of Fig. 1 and add them up over the first 500 years. The result is 0.003 deaths, most of them in the first 100 years. However, this ignores all the time delays and special protections during this early time period that were outlined above: geologists feel confident that no groundwater will intrude into the waste repository for at least a thousand years; the corrosion-resistant casing is virtually impregnable for several hundred years; it takes groundwater a thousand years to get to the surface; and so on. Moreover, since it is quite certain that some sort of surveillance would be maintained during this period, any escaping radioactivity would be detected in plenty of time to avert health problems. These factors reduce the dangers at least 30-fold, to no more than 0.0001 deaths. This is close to a million times less then the number of deaths due to air pollution from coal burning.
The chemical carcinogens released into the ground in coal burning do about 1 percent of their damage during the first 500 years; we may consequently expect 0.5 deaths in that period. With a 500-year perspective, there is no need to consider the much later effects of the coal reaching the surface by erosion if it had not been mined. We see that the effects of chemical carcinogens from coal burning are 5,000 times worse than those of nuclear waste (0.5 / 0.0001).
By similar reasoning, the chemical carcinogens from solar electricity will cause 0.015 deaths due to the coal used in making materials for it; if cadmium sulfide solar cells are used, they will cause 0.8 deaths. Again these are far greater than the 0.0001 deaths due to the waste from nuclear power.
As a consequence of public fear, siting a repository for high-level waste has become a very difficult and expensive process. The NIMBY syndrome — Not in my back yard — receives its fullest expression here because there is little obvious benefit and enormous perceived harm to the area that accepts the waste. There is even a stigma attached to being the place where the nation's "atomic garbage" is sent. The issue is made to order for local environmental groups. By opposing the repository they get lots of media coverage, which is the essential ingredient needed for them to prosper. The issue is also made to order for local politicians who can garner lots of votes by posing as the defender of the home territory against the intrusion of the federal government and the commercial interests of the rest of the nation. There are few votes to be gained by supporting the local siting of a repository.
The U.S. Department of Energy (DOE), which is charged with the responsibility for managing the waste, has faced this difficult situation by adopting the position that repository site selection is strictly a scientific problem, requiring a tremendous research effort which it is more than happy to undertake. The money for it is available from the 0.1 cent per kilowatt-hour tax on nuclear electricity. Through 1989, $6 billion had already been collected. Managing a large research program is clearly advantageous to the careers of those in charge, and it also delays the pain of making a decision. The longevity of individuals in top government positions is such that they personally will probably never have to make a final decision — for a government bureaucrat that is the ideal situation.
As a result of these factors, selection of a repository site has been painfully slow. The current status is that a tentative site has been selected, under Yucca mountain in Nevada, 100 miles northwest of Las Vegas, and research is proceeding to determine whether it is suitable. The research plan, published in December 1988, runs more than 6,300 pages and cost $30 million! The research project itself was estimated to take 7 years and cost $2 billion. It was to include drilling and blasting two shafts 1,000 feet deep to the repository level, and carving out an underground laboratory there for carrying out experiments that simulate the underground environment. In addition, there were to be over 300 drill holes to explore the geology and hydrology beyond the laboratory.
A year later, the new Secretary of Energy decided that the entire research plan should be revised. As part of the new procedure, the repository will not become operational until 2010.
Yucca mountain is in a very barren desert region, adjacent to the nuclear weapons testing facility, an area larger than the state of Rhode Island known as the Nevada Test Site (NTS). The NTS itself was originally part of, and along with Yucca mountain is still surrounded by, a much larger U.S. Air Force bombing and gunnery range.
Because of the NTS, radioactivity is not a stranger to the area. About 100 nuclear bomb tests were conducted in the atmosphere there between 1951 and 1963, and since 1963, 600 more announced tests have been conducted underground. Additional tests were not announced to the public. In the late 1980s, an average of 14 tests per year were announced. Each underground bomb test can be considered as a miniature high-level waste repository.
One can stand on high ground overlooking Frenchman's Flat and see many dozens of craters, each caused by surface subsidence above a cavity caused by an underground nuclear explosion. One can see heavily damaged buildings and bridges exposed to the earlier tests in the atmosphere. The most spectacular sight is Sedan crater, 1,280 feet in diameter and 320 feet deep, created in a test of the potential use of nuclear bombs for large excavation projects — that one bomb removed 12 million tons of earth. But most testing is now conducted in "rooms" leading off of tunnels drilled into the sides of mountains.
Yucca mountain is several miles away from the part of NTS used for bomb testing. The NTS areas nearby have been used for testing nuclear reactors developed for spaceship propulsion, a project that has now been abandoned. Any possible effects of the bomb testing on the security of the waste repository will be carefully considered.
The rock under Yucca mountain is welded tuff, a volcanic lava which oozed out of the earth 13 to 18 million years ago and remained at high temperature and out of contact with air for a long time. This caused it to become tightly welded into a dense, nonporous rock.
Yucca mountain is one of the driest places in the United States, with only 6 inches of rainfall per year, only 5% of which (0.3 inches per year) soaks into the ground. The water table is more than 2,500 feet deep, so that the 1,200-foot-deep repository will be 1,300 feet above it. Only a tiny amount of moisture can therefore contact the buried waste. The rock below the repository is especially rich in zeolites, materials with chemical properties that make them efficient at absorbing dissolved radioactive materials out of water passing through. It is estimated that water percolating down would take 2,000-8,000 years to travel this 1,200 feet from the repository to the water table.
If any radioactive waste should be dissolved out, and if it should somehow escape adsorption in the zeolites and reach the water table, consequences would still be minimal. Groundwater in the region moves especially slowly, only about 1 foot per year! The nearest place it could reach the surface is 30 miles away — 150,000 years at 1 foot per year — in the Amargosa desert, which is a closed drainage basin — water flowing into it stays there until it evaporates. Note that the 1 foot per year flow rate applies to the water; as explained previously, materials dissolved in it move hundreds or thousands of times more slowly. For them to travel 30 miles would take many millions of years!
In summary, there is virtually no moisture to dissolve the waste, which is in any case in insoluble form and protected by casings and backfill material. If any material is dissolved, the only escape path is downward 1,300 feet to the top of the water table through rock that is highly efficient at adsorbing out the dissolved materials. If it should reach the water table it would take many millions of years to reach the surface, and that would leave it trapped in the middle of a virtually uninhabited desert with no way to get out. Note that this is very much safer than the situation assumed in our risk analysis above for average underground conditions in which the waste is submerged in groundwater (i.e., below the top of the water table) that moves at a velocity of 1 foot per day, and flows into a river through a region of U.S. average population.
There are other matters to consider, including the potential effects of climate change, volcanoes, and earthquakes. All of these now seem to be of minimal concern. The closest major earthquake was 90 miles to the west in 1872, and there has been no major faulting or folding of rocks for over 10 million years. The climate has been arid for over 2 million years, and there have been no volcanoes for several million years. But investigating these matters is an important part of the research program.
In spite of all this, the Las Vegas area, which has lived with nuclear bomb testing at similar or closer distances for nearly 40 years, is alive with opposition, including citizens' alliances, residents' coalitions, governor's commissions, study committees, and the like. They are composed of ordinary people — secretaries, teachers, iron workers, printers, lawyers, real estate brokers. In accordance with the law, some of these are funded by the DOE out of funds from the tax on nuclear electricity. They say that, in accepting the nuclear bomb testing facility, Nevada has done its share, so some other state should accept the nuclear waste.
Nevada's governors and senators have opposed the repository. The state legislature passed resolutions opposing it, refusing to yield jurisdiction and withholding consent. It even passed a law making it a crime for anyone to store high-level radioactive waste in the state punishable by fines and imprisonment. That law is being tested in the courts. The state has filed several law suits against the DOE, and the legal situation is cluttered with countersuits and appeals.
Some Nevadans favor the repository as a diversification of industry for the state, which is highly dependent on tourism and gaming. Some fears have been expressed that other industries may be deterred from moving to the area, but in 1988-89, 50 businesses moved into Nevada and none raised the repository issue as a concern. Some Nevadans are more concerned with negotiating the best possible deal in terms of payments from the DOE for accepting the repository. There is every indication that the state will be well compensated.
If the legal problems can be worked out, and if the technical evaluation of the site does not encounter serious problems, the Yucca mountain repository will be built and operating by about the year 2010. The cost will be tremendous, but it will be covered by the 0.1 cent per kilowatt-hour tax which adds only 1% to the cost of nuclear electricity.
WHY THE PUBLIC FEAR?
If the picture I have presented in this chapter is correct, does not omit important aspects of the problem, and is not misleading, it is difficult for me to understand why people worry about the dangers of high-level radioactive waste. The material presented here has been published in the appropriate scientific journals for some time. It had been approved by scientific referees and editors to get there. There have been no critiques of it offered. I have presented it at international, national, and regional scientific conferences, and in seminar talks at several major universities, all without receiving substantive criticisms or adverse comments. I therefore know of no evidence that my treatment is not a correct and valid assessment of the problem based on scientific analyses.
There have been other scientific analyses of the high-level radioactive waste hazards using very different approaches that I believe to be less valid than mine, but they come out with rather similar results.9 They also find the health effects to be trivial.
Why, then, is there so much opposition? What is the basis for the public worry about this problem? There have been a few scientific papers that concoct very special scenarios in which substantial — but still far from catastrophic — harm to public health might result, but they never attempt to estimate the likelihood of their scenarios. All of them are obviously extremely improbable. Note that in my treatment the probabilities of all scenarios are automatically taken into account as long as they apply equally to average rock.
Nevertheless, there can be no question but that the fear abounds. A segment on a network TV morning show opened with the statement "[this waste] could possibly contaminate the environment. The result, of course, would be too horrible to contemplate; it could eventually mean the end of the world as we now know it." I cannot imagine any situation in which this last statement is meaningful short of feeding all of the people in the world directly with the waste. As has been pointed out, there are many other substances that would serve with greater effectiveness if this were done.
Probably the best evidence for this fear is that our government is willing to spend huge sums of money on the problem. The fear is surely there. Perhaps the most important reason for it is that disposal of high-level waste is often referred to as an "unsolved problem." When people say this to me, I ask whether disposal of the waste from coal burning — releasing it as air pollution, killing about 30,000 Americans each year — is a "solved problem." They usually say "no" but add that air pollution is being reduced. Actually we can hardly hope to reduce it to the point of killing fewer than 5,000 Americans per year. It is therefore difficult to understand how that converts it into a "solved problem." When I point out that the radioactive waste problem is not unsolved, since there are many known solutions, the usual retort is "then why aren't we burying it now?" The answer to that question is we are in the process of choosing the best solution. This is about as far as the discussion goes, but the real difficulty is that it rarely goes that far. The great majority of people are still hung up on "it's an unsolved problem."
I like to point out that nobody is being injured by the high-level waste, and there is no reason to believe that anyone will be injured by it in the foreseeable future — compare this with the 30,000 deaths per year from the wastes released in coal burning. The usual reply is "how do you know that nobody is being injured?" The answer is that we constantly measure radiation doses in and around nuclear facilities and throughout our environment, and nobody is receiving any such doses from high-level waste. If there is no radiation dose, there can be no harm. I don't believe any scientist would argue this point, but I'm sure most people continue to believe that high-level waste (or the spent fuel from which it is to be derived) actually is doing harm now.
The real difficulty with public understanding of the high-level waste problem is that the scientists' viewpoint is not being transmitted to the public. Transmitting information from the scientific community to the public is in the hands of journalists, who have chosen not to transmit on this question. I'd hate to speculate on their motives, but they are doing great damage to our nation. These are the same journalists who constantly trumpet the claim that the government is suppressing information on nuclear energy. What more despicable suppression of information can there be than refusing to transmit the truth about important questions to the public? It's every bit as effective as lying.
CHAPTER 11 APPENDIX
Probabilities for Entering the Human Body10
We inhale about 20 cubic meters (m3) of air per day, or 7,000 m3 per year. Dust levels in air from materials on the ground becoming suspended are about 35 x 10-6 g/m3. Thus we inhale (20 x 35 x 10-6 =) 0.7 x 10-3 grams per day of material from the ground, or 0.25 grams per year.
The area of the United States is about 1013 m2, so the volume of the top inch (0.025 m) of soil is (.025 x 1013 =) 2.5 x 1011 m3. Since the density of soil is 2 x 106 g/m3, this soil weighs (2 x 106 x 2.5 x 1011 =) 5 x 1017 grams. Since each person inhales 0.25 g/yr of this soil, the quantity inhaled by the U.S. population (240 x 106) is (240 x 106 x 0.25 =) 6 x 107 g/yr. The probability for any one atom in the top inch of U.S. soil to be inhaled by a human in one year is therefore (6 x 107/5 x 1017 =) 1.2 x 10-10, a little more than 1 chance in 10 billion.
The probability for an atom in a river to enter a human is very much larger. The total annual water flow in U.S. rivers is 1.5 x 1015 liters, whereas the total amount ingested by humans is (2.2 liters/person per day x 365 days/year x 240 x 106 = 1.8 x 1011 liters per year. Thus the probability for an atom in a river to be ingested by a human is (1.8 x 1011/1.5 x 1015 =) 1.2 x 10-4, or a little more than 1 chance in 10,000 per year.
Radiation Reaching the Surface from Buried Waste
Rock and soil attenuate gamma rays, the most penetrating radiation from radioactive waste, by more than a factor of 3 per foot. Since the waste will be buried 2,000 feet underground, gamma rays from it would be attenuated by a factor of 32000 = 101000, an enormously large number. The radioactive waste produced by a million years of all-nuclear power in the United States would eventually emit about 1036 gamma rays;11 thus the probability of even a single gamma ray from it reaching the surface would be about (1036/101000 =) 10-964, an infinitesimally small probability (964 zeros after the decimal point).
Derivation8 of Fig. 1, Chapter 11
For illustrative purposes, let us calculate the number of liver cancers expected from people eating 1 millicurie (3.7 x 107 radioactive decays per second) of plutonium-239 (239Pu) that is present in the waste.2 Since the radiation emitted by 239Pu, called alpha particles, does not go very far — it can barely get through a thin sheet of paper — this material can cause liver cancer only if it gets into the liver. Experiments indicate that 0.01% of ingested 239Pu gets through the walls of the gastrointestinal tract into the bloodstream, and of this, 45% is deposited in the liver; thus (3.7 x 107 x 0.0001 x 0.45 =) 1,700 alpha particles strike the liver each second. Since 239Pu remains in the liver for an average of 40 years (1.2 x 109 seconds), the total number of alpha particles that eventually strike the liver is (1,700 x 1.2 x 109 =) 2 x 1012. This is multiplied by the energy of the alpha particle to give the energy deposited, 1.5 joules, which is then divided by the mass of the liver, 1.8 kg, and multiplied by a conversion factor to give the dose in millirem, 1.6 x 106. The risk of liver cancer per millirem of alpha particle bombardment is estimated from studies of patients exposed for medical purposes to be 0.015 x 10-6 per millirem. The number of liver cancers expected from eating 1 millicurie of 239Pu is therefore (1.6 x 106 x 0.015 x 106 =) 0.024. Since the waste produced in one year by one plant contains 6 x 104 millicuries of 239Pu, the number of liver cancers expected if this were fed to people would be (6 x 104 x 0.024 =) 1,400.
But once 239Pu gets into the bloodstream, it can also get into the bone — 45% accumulates there, and it stays for the remainder of life; it therefore can cause bone cancer. A calculation like that outlined above indicates that 700 cases are expected. When other body organs are treated similarly, the total number of cancers expected totals 2,300, which is the value of the curve labeled "239Pu" in Fig. 1 in early time periods.
The quantity of 239Pu in the waste does not stay constant, for two reasons. Every time a particle of radiation is emitted, a 239Pu atom is destroyed, causing the quantity to decrease. But 239Pu is the residue formed when another radioactive atom, 243americium, emits radiation, which adds to the quantity. When these two effects are combined, the quantity versus time is as shown by the curve in Fig. 1.
There are many other radioactive species besides 239Pu in the waste; similar curves are calculated for them and shown in Fig. 1 (Chapter 11. The total number of cancers is then the sum of the number caused by each species, which is obtained by adding the curves at each time. The result is the thick curve above all the others in Fig. 1 (Chapter 11). That is the curve used in our discussions as the number of cancers expected if all the waste produced by one power plant in one year were fed to people in digestible form.
Probability for an Atom of Rock to Enter a Human Stomach15,***
From the measured rate at which rivers carry dissolved material into oceans, it is straightforward to calculate that an average of 1.4 x 10-5 meters of depth is eroded away each year. Hydrologists estimate that 26% of this erosion is from dissolution of rock by groundwater; the rest is from surface water. Thus (0.26 x 1.4 x 10-5 =) 3.6 x 10-6 meters of depth are dissolved annually by groundwater. The fraction of this derived from 1 meter of depth at 600 meters below the surface may be estimated from our knowledge of how groundwater flow varies with depth; it is about 2.6 x 10-4. The total amount of rock derived from our 1 meter of depth in 1 year is then (3.6 x 10-6 x 2.6 x 10-4 =) 1 x 10-9 meters per year. If 1 x 10-9 meters is removed from 1 meter of depth each year, the probability for any one atom to be removed is 1 x 10-9, one chance in a billion per year. This result applies to all rock, averaged over the continent.
We now provide an alternative derivation for an atom of rock which is submerged in groundwater. Consider a flow of groundwater, called an aquifer, along a path through average rock and eventually into a river. There is a great deal of information available on aquifers, like their paths through the rocks, the amount of water they carry into rivers each year, and the amounts of various materials dissolved in them. From the latter two pieces of information, we can calculate the quantity of each chemical element carried into the river each year by an average aquifer — i.e., how much iron, how much uranium, how much aluminum, and so on.
Where did this iron, uranium, and aluminum in the groundwater come from? Clearly, this material was dissolved out of the rock. From our knowledge of the path of the aquifer through the rock and the chemical composition of rock, we know the quantity of each of the chemical elements that is contained in the rock traversed by the aquifer. We can therefore calculate the fraction of each element in the rock that is dissolved out and carried into the river each year. For example, a particular aquifer may carry 0.003 pounds of uranium into a river each year that it dissolved out of a 50-mile-long path through 200 million tons of rock that contains 1,000,000 pounds of uranium as an impurity (this is typical of the amount of uranium in ordinary rock). The fraction of the uranium removed each year is then 0.003/1 ,000,000, or 3 parts per billion. Similar calculations give 0.3 parts per billion for iron, 20 parts per billion for calcium, 7 parts per billion for potassium, and 10 parts per billion for magnesium. To simplify our discussion, let us say that lO parts per billion of everything is removed each year — this is faster than the actual removal rates for most elements. This means that the probability for any atom to be removed is 10 chances in a billion each year. This is 10 times larger than our first estimate, 1 chance in a billion. This is partly explained by the fact that most rock is not submerged in groundwater, as we have assumed here. But the important point is that we have given two entirely independent derivations and have arrived at roughly the same result. To be conservative, we will use the higher probability, 10 chances in a billion per year. Incidentally, this result implies that for ordinary rock submerged in groundwater, only 1% is removed per million years [ (10/1 billion) x 1 million = 0.01], so it will typically last for 100 million years.
It was shown in the first section of this Appendix that an average molecule of water in a river has 1 chance in 10,000 of entering a human stomach before flowing into the oceans. For materials dissolved in the water, the probability is somewhat smaller because some of it is removed in drinking water purification processes, but the probability is increased by the fact that some material in rivers finds its way into food and enters human stomachs by that route. These two effects roughly compensate one another. We therefore estimate that material dissolved in rivers has 1 chance in 10,000 of getting into a human stomach.
Since an atom of the rock has 10 chances in a billion of reaching a river each year, and once in a river has 1 chance in 10,000 of reaching a human stomach, the overall probability for an atom of the rock to reach a human stomach is the product of these numbers [(10/1 billion) x (1/10,000) = ], 1 chance in a trillion per year. That is the value used in our discussion.
In considering effects of erosion, we assumed that all the waste would be released into rivers after 13 million years. According to Fig. 1 in Chapter 11, if all the waste remaining at that time were to get into human stomachs, about 40 deaths would be expected. But we have just shown that if the material is released into rivers, only 1 atom in 10,000 reaches a human stomach; we thus expect (40/10,000 =) 0.004 deaths. That is the result used in our discussion.
*From our experience with tumblers, jars, and trinkets, we think of glass as fragile, but a large block of solid glass is not much more fragile than most rocks. Both can crack and chip when forces are applied but this does not greatly affect their underground behavior since there are powerful pressures holding the pieces together.17
**We have shown that the average erosion rate is one meter every 22,000 years. We imply here that most of the materials ends up within something like 4.5 meters (15 feet) of the surface (4.5 x 22,000 = 100,000).18
***For example, if feeding a quantity of waste to a thousand people would give each person a risk of 1/10, we would expect (1000 x 1/10 =) 100 deaths; but if instead the quantity were fed to 10,000 people, each would eat one-tenth as much and hence have a risk of only 1/100, so we would expect (10,000 x 1/l00 =) 100 deaths, the same as before.19